Multi-access edge computing (MEC) has attracted lots of research interests from both academic and industrial fields, which aims to extend cloud service to the network edge to reduce network traffic and service latency. One key decision-making problem in MEC systems is task offloading which aims to decide which tasks should be migrated to the MEC server to minimize the running cost. In this article, I am going to talk about how to use learning-based methods to address the above problem.

An overview of Multi-access edge computing

The technological evolution of smartphones, tablets, and wearable devices is driving the emergence of novel computationally demanding services and applications such as virtual reality (VR), augmented reality (AR), face recognition, and mobile healthcare. Although new generations of mobile devices possess more computing power, they are still unable to run the computation-intensive applications efficiently. To resolve this issue, Multi-access Edge Computing (MEC), a key technology in the fifth-generation (5G) network, was proposed to meet the ever-increasing demands for the Quality-of-Service (QoS) of mobile applications. MEC provides many computing and storage resources at the network edge (close to users), which can effectively cut down the application latency and improve the QoS.

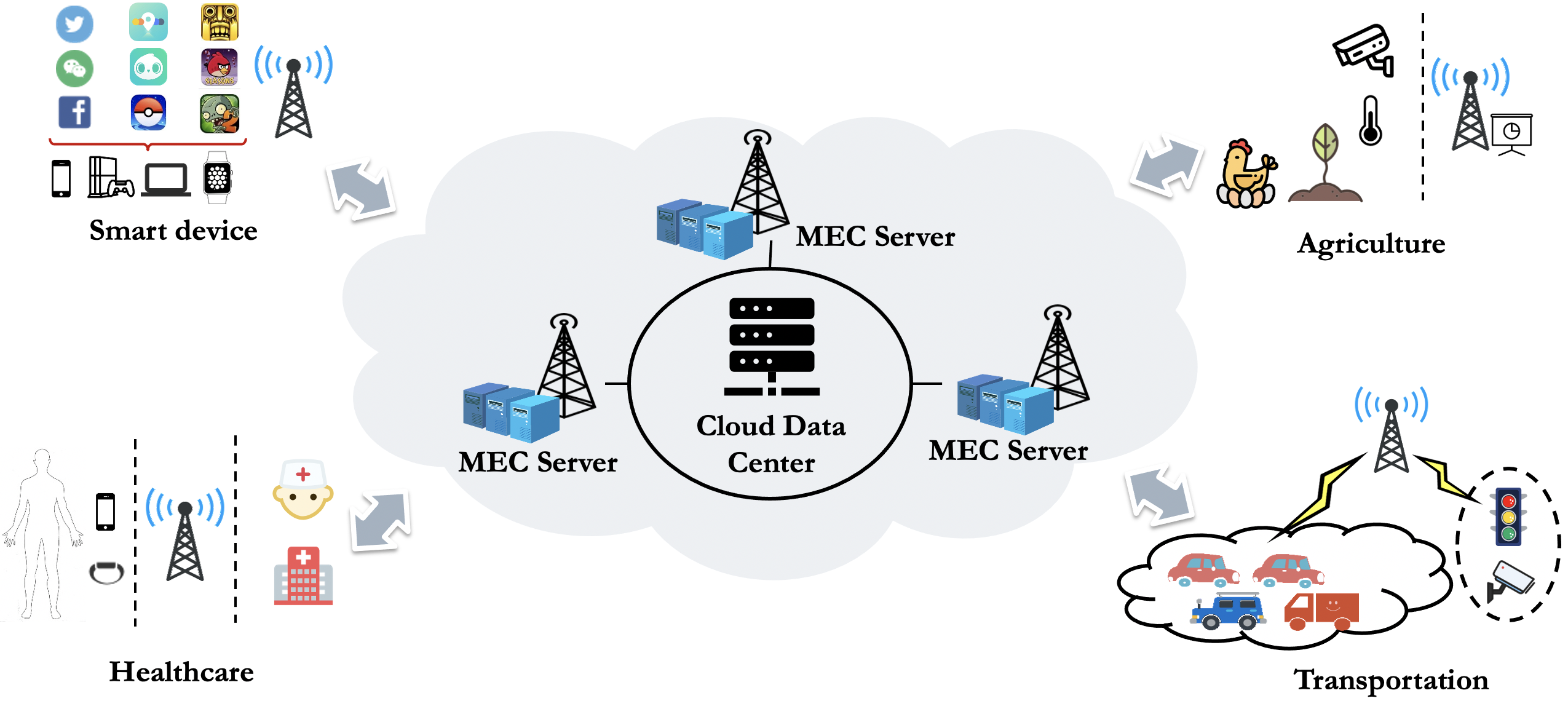
MEC-system application

Fig. 1 MEC system architecture.

Numerous MEC applications have emerged in different areas, which improve the quality of living and enhance productivity. Meanwhile, a variety of applications such as social networking, gaming, and AR become increasingly complex, and therefore demand more computing resources and energy. In the definition of the ESTI, a MEC system generally consists of tree levels: user level, edge level, and remote level. Here, the user level includes heterogeneous user devices, the edge level contains MEC servers that provide edge computing services, and the remote level consists of cloud servers. Specifically, mobile users communicate with an MEC server through the local transmission unit. The edge level incorporates a virtualization infrastructure that provides the computing, storage, and network resources.

Task offloading in MEC

Task offloading is to decision what tasks should be offloaded from the user devices to the MEC server so that the total running cost is minimal. In general, there are two task models used in the related work: task model for binary offloading and that for partial offloading according to a survey paper. In the task model for binary offloading, there are no inner dependencies among computation tasks for a mobile application. In contrast, mobile applications are composed of tasks with inner dependencies in the task model for partial offloading, which is able to achieve a fine granularity of computation offloading, leading to better offloading performance. Hence, we consider task model for partial offloading.
example

Fig. 2 An example of task offloading.

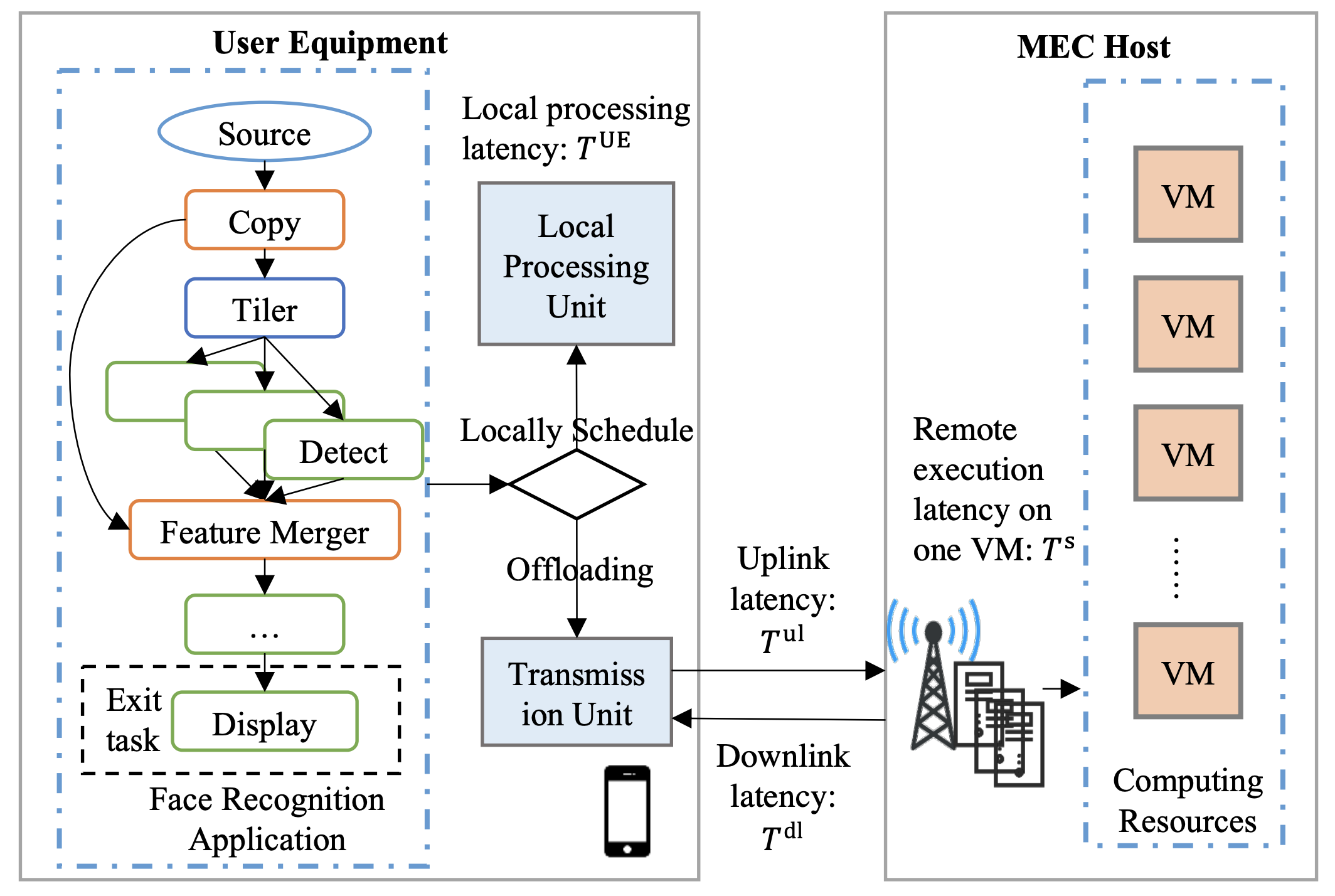
The above figure shows a typical example of the task offloading in MEC system. This example considers a real-world application—face recognition, which consists of dependent tasks such as tiler, detection, or feature mergence. The mobile device makes offloading decisions for those tasks according to the system status and task profiles, thus some tasks are run locally on the mobile device while others are offloaded to the MEC host via wireless channels. Typically, the mobile application can be modelled as Directed Acyclic Graph (DAG), where the vertex set represents the tasks and the directed edge set represents the dependencies among tasks, respectively. The task offloading problem can then be converted to specific DAG scheduling problem with the MEC environment. However, this problem is hard to solve due to the NP-hardness. Traditional solutions for the NP-hard problem requires considerable human expert knowledge to design and tuning the heuristic rules of the algorithm, which might hard to fast adapt to dynamic scenarios arisen from increasing complexity of applications and architectures of MEC. To address the above challenging, Reinforcement learning based algorithms are promising which learn to solve complex decision-making problems based on the interaction with the target environment.

Reinforcement Learning based task offloading in MEC

In order to design reinforcement learning based task offloading method, we need to tailer the components of the RL including state space, action space, reward function, representation of the policy, etc. according to the task offloading problem. Let us first review basic concept of reinforcement learning.

A Brief Introduction of Reinforcement Learning

RL considers learning from environment so as to maximize the accumulated reward. Formally, a learning task, $\mathcal{T}$, is modelled as an MDP, which is defined by a tuple $( \mathcal{S}, \mathcal{A}, \mathcal{P}, \mathcal{P}_0, \mathcal{R}, \gamma )$. Here, $\mathcal{S}$ is the state space, $\mathcal{A}$ denotes the action space, $\mathcal{R}$ is a reward function, $\mathcal{P}$ is the state-transition probabilities matrix, $\mathcal{P}_0$ is the initial state distribution, and $\gamma \in [0, 1]$ is the discount factor. A policy $\pi(a \mid s)$, where $a \in \mathcal{A}$ and $s \in \mathcal{S}$, is a mapping from state $s$ to the probability of selecting action $a$. We define the trajectories sampled from the environment according to the policy $\pi$ as $\tau = (s_0, a_0, r_0, s_1, a_1, r_1, …)$, where $s_0 \sim \mathcal{P}_0$, $a_t \sim \pi( … \mid s_t)$ and $r_t$ is a reward at time step $t$.

The state value function of a state $s_t$ under a parameterized policy $\pi(a \mid s; \theta)$, denoted as $v_{\pi}(s_t)$, is the expected return when starting in $s_t$ and following $\pi(a \mid s; \theta)$ thereafter. Here, $\theta$ is the vector of policy parameters and $v_{\pi}(s_t)$ can be calculated by

\[v_{\pi}(s_t)=\mathbb{E}_{\tau \sim P_{\mathcal{T}}(\tau \mid \theta)}\left[ \sum_{k=t}\gamma^{k-t} r_k \right]\]

where $P_{\mathcal{T}}(\tau \mid \theta)$ is the probability distribution of sampled trajectories based on $\pi(a \mid s; \theta)$. The goal for RL is to find an optimal parameterized policy $\pi(a \mid s; \theta^*)$ to maximize the expected total rewards $ J = \sum_{s_0 \sim \mathcal{P}_0} v(s_0)$.

Reinforcement Learning based Task offloading

The above task offloading problem is a typical combinatorial optimization problem, inspired by some early works that use sequence-to-sequence (seq2seq) neural network to solve combinatorial problem (pointer network, RL+pointer network), our core idea is to convert the task offloading into a sequence-to-sequence decision-making problem, where the input is a sequence of tasks and the output is the decisions of the tasks. 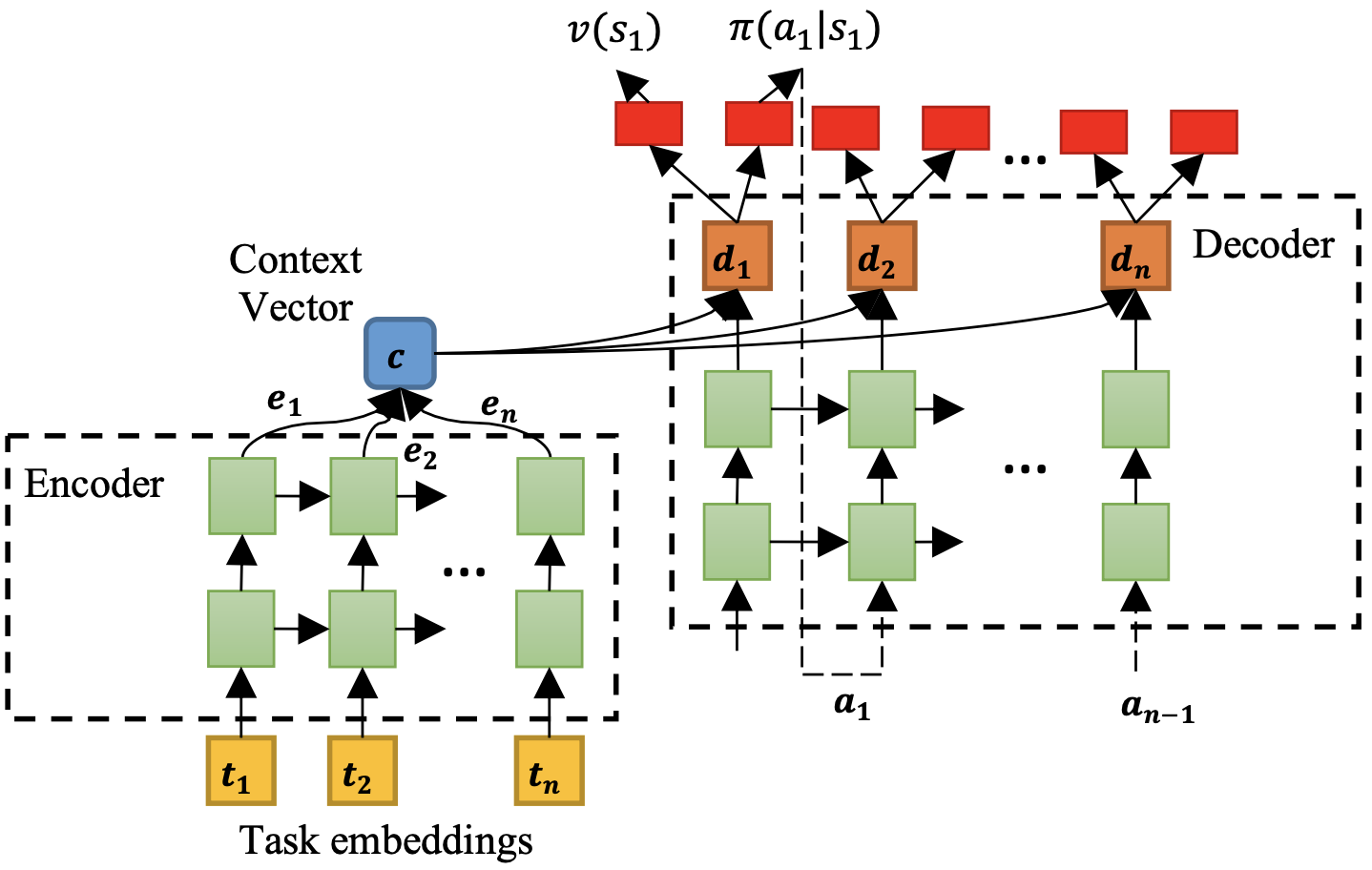The offloading policy is represented by a seq2seq neural network as follows: example

Fig. 3 The structure of sequence to sequence neural network.

The policy network is a typical encoder-decoder architecture, where both encoder and decoder are Long Short-Term Memory (LSTM). The encoder aims encoder the DAG information and decoder aims to output offloading decisions for tasks. To better extract features from the DAG, the encoder can be replaced by Graph Neural Network (GNN) which shows good representing performance handling graph data.

After we choose the right model to represent the policy, the next issue we need to solve is how to train the policy network in MEC system? Considering different mobile users may have different preference of mobile applications, it is better to obtain personlized policy for mobile users rather than obtaining a global policy for all users. Besides, considering the limited computation resources and local data of mobile users, we need to improve the training efficiency on mobile devices. To address the above issue, Meta Reinforcement Learning (MetaRL) is an appealing solution.

MetaRL aims to learn policies for new tasks within a small number of interactions with the environment by building on previous experiences. In general, MRL conducts two “loops” of learning, an “outer loop” which uses its experiences over many task contexts to gradually adjust parameters of the meta policy that governs the operation of an “inner loop”. Based on the meta policy, the “inner loop” can adapt fast to new tasks through a small number of gradient updates (here is a very good paper to describe MRL). To make it concrete, we follow the formulation of model-agnostic meta-learning (MAML), giving the target of MRL as:

\[J(\theta) = \mathbb{E}_{\mathcal{T}_i \sim \rho(\mathcal{T})} \left [ J_{\mathcal{T}_i}(\theta') \right ], {\rm with} \ \theta' := U(\theta, \mathcal{T}_i),\]

where $\mathcal{T}$ represents a learning task, $\rho(\mathcal{T})$ represents the distribution of learning tasks, and $\theta$ represent the parameters of the policy network. $U$ represents the update function, for instance, if we conduct $k$-step gradient ascent for $\mathcal{T}$, then $U(\theta, \mathcal{T}) = \theta + \alpha\sum_{t=1}^k g_t$, where $g_t$ denotes the gradient of $J_{\mathcal{T}_i}$ at time step $t$ and $\alpha$ is the learning rate.

Therefore, the optimal parameters of policy network and update rules are

\[\begin{equation} \label{MRL-update} \begin{aligned} & \theta^{*} = {\rm argmax}_{\theta} \mathbb{E}_{\mathcal{T}_i \sim \rho(\mathcal{T})} \left [ J_{\mathcal{T}_i}(U(\theta, \mathcal{T}_i) \right ], \\ &\theta \leftarrow \theta + \beta \mathbb{E}_{\mathcal{T}_i \sim \rho(\mathcal{T})} \left [ \nabla_{\theta}J_{\mathcal{T}_i}(U(\theta, \mathcal{T}_i) \right ], \end{aligned} \end{equation}\]

where $\beta$ is the learning rate of “outer loop” training.

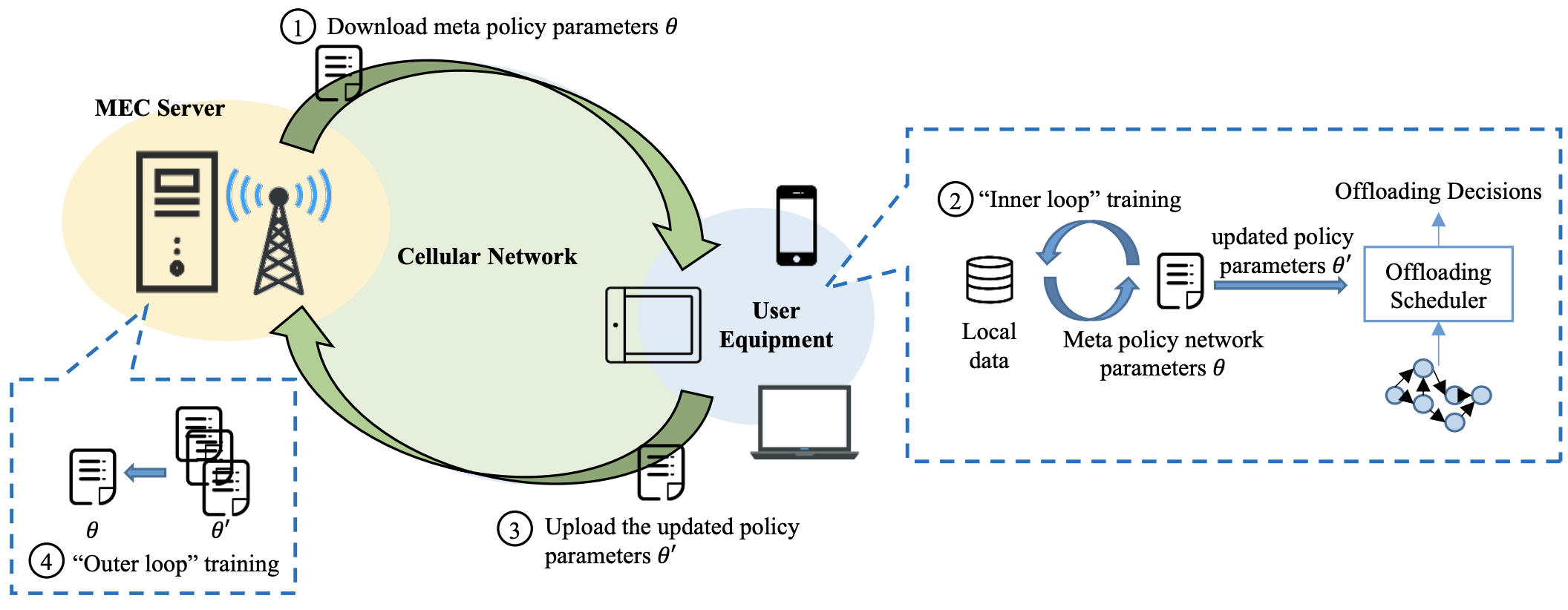
example

Fig. 4 Integrating meta reinforcement learning with MEC.

This “inner-outer loop” training scheme can be perfectly integrated into the MEC system, where the “outer loop” is conducted on the edge server to obtain the meta offloading policy for all mobile users and the “inner loop” training can be conducted by the mobile user to get the personalized offloading policy. As shown in Fig. 4, the training process includes four steps. First, the mobile user downloads the parameters of the meta policy from the MEC server. Next, an “inner loop” training is run on every mobile device based on the meta policy and the local data, in order to obtain the personalized policy. The mobile user then uploads the parameters of the personalized policy to the MEC server. Finally, the MEC server conducts an “outer loop” training based on the gathered parameters of personalized policies, generates the new meta policy, and starts a new round of training. Once obtaining the stable meta policy, we can leverage it to fast learn a personalized policy for new mobile user through “inner loop” training. Notice that the “inner loop” training only needs few training steps and a small amount of data, thus can be sufficiently supported by the mobile devices.

This post is based on the following papers: